Pitágoras Cultor de la inteligencia Visual

julio 22, 2025

Pitágoras Cultor de la inteligencia Visual

Posted by Estudio de Arqué Poética y Visualística Prospectiva on julio 22, 2025 in Argumentario, Estudio Arqué Poética y Visualística Prospectiva

0 Comments

Pitágoras Cultor de la inteligencia Visual / Espacial

de las Formas y de los Números

Imaginante de Taxografías

Las formas son: representaciones de ideas, relaciones y visualización de propósitos…
Los números son: instrumentos para cuantificar, organizar, ubicar y especular, amén de…

PITÁGORAS

Ve la luz en la isla de Samos, perla del mar Egeo, en el 572 a.C.

Filósofo, matemático, astrónomo y médico; exiliado, fallece en Metaponto en el 497 a.C., a pesar de ser reconocido como una de las cumbres del pensamiento helénico.

Por la luminosa multifonía hipercromática de las visiones y de las proféticas demostraciones sin palabras del hijo dilecto de Samos, patrono del pensamiento de Occidente.

La demostración del teorema para la obtención del ángulo recto sexagesimal y el helenocentrismo se atribuyen a Pitágoras de Samos. La aplicación y utilización de este conocimiento para satisfacer diversos menesteres de la vida pertenece a las ancestrales culturas autoras y mentoras de la tradición occidental. La academia por él fundada impulsó el desarrollo de las matemáticas en la antigua Grecia. La significación de Pitágoras también se distingue en el ámbito del devenir de las IDEAS universales: su pensamiento, consecuente con sus circunstancias, está matizado por el misticismo y el esoterismo de las antiguas religiones y filosofías del Extremo y Medio Oriente.

Es iniciador de secuencias de temáticas e interrogantes que, tamizadas por los legendarios Sócrates y Platón, constituyeron la tradición filosófica y científica de Occidente.

Pitágoras de Samos, hijo del próspero mercader Mnesarco, tuvo un comprensivo progenitor que lo alentó a realizar su ser y sus sueños, adelantándole su herencia. Esta herencia le procuró los medios suficientes para viajar a Mileto y después residir en Fenicia y Egipto, cunas del conocimiento esotérico y precientífico. El joven Pitágoras pudo observar misteriosas manifestaciones en esas latitudes, así como conocer los preceptos de sus geometrías, astronomías y artes de la sanación.

Se infiere que Pitágoras se estableció en Babilonia para estudiar allí los orígenes de los saberes aritméticos, numerológicos, geométricos (taxográficos), cronométricos, calendáricos y fonoeurítmicos (musicales).

Se menciona que viajó a Crotona, donde fundó su emblemática academia. Su comunidad se convirtió en una eminente fuerza política aristocratizante que provocó la violenta animadversión de varias facciones del conglomerado demócrata, las cuales lo hostigaron reiteradamente. Por ello, Pitágoras se autoexilió los últimos años de su admirada y luminosa vida en el Museion de Metaponto.

Pitágoras, como la gran mayoría de los pensadores de esa época, no dejó obra escrita, por lo que es imposible distinguir las ideas y descripciones del magno maestro de las de sus subsecuentes discípulos, sus posteriores intérpretes, las múltiples traducciones y las innumerables versiones de ulteriores trasfondos culturales: latino, bizantino, arábigo, magrebí, andalusí, toledano, toscano, véneto, lombardo, piamontés, galo, británico, germánico.

Uno de los posibles periplos al conocimiento para el pensador Pitágoras fue lo que él denominó filosofía, disciplina cognitiva de dimensiones discursivas, analíticas, especulativas, reflexivas y argumentativas, además de ser vista en sentido literal como “amor a la sabiduría”. Cuando el tirano Leonte de Fliunte le preguntó si se consideraba un hombre sabio, Pitágoras de Samos le respondió cortésmente que era un filósofo, un apasionado amante de todos los conocimientos.

Pitágoras de Samos es amante y cultor de conocimientos, sagaz estudioso de los devenires y porvenires de la humanidad. Se le atribuye haber concebido y visualizado las matemáticas como una disciplina abstracta y liberal, no solo como un instrumento pragmático, como otrora lo fue la agrimensura faraónica. Mediante la formulación abstracta de sus resultados, con independencia del contexto material y con una naturaleza propia en su forma de objeto mental.

Recientemente, la arqueología ha realizado acuciosos análisis de varios testimonios materiales de primigenias civilizaciones tan disímiles como las chinas, las indostánicas, las sumerias, las egipcias, las persas, las mayas, las andinas y las anasazi. Estas ya conocían los valores de la posteriormente llamada terna pitagórica y su utilización práctica mediante la consecución del ángulo recto sexagesimal para determinar áreas, altitudes, orientaciones y como referencia para explorar los cielos, edificar viviendas, templos, proyectar caminos y acequias, así como para calendarizar rituales propiciatorios y prever escenarios climáticos con el fin de determinar estrategias agrícolas.

Sin embargo, se atribuye a Pitágoras la primera demostración del teorema que describe la ortogonalidad sexagesimal, así como ser el timón de las aportaciones de los profesantes de sus legendarias hipótesis y tesis, que son la simiente teórica para las acepciones de las disciplinas matemáticas y para su universalización mediante representaciones visuales.

Un teorema matemático que visualiza su demostración en diversas circunstancias es parangón para ejemplificar el método pitagórico en el arduo logro de la purificación y perfección del alma. En el mismo tópico, se consideró como una guía para acceder a la comprensión y al conocimiento del mundo como preeminente expresión de sublime armonía.

Pitágoras intuía al universo en forma de cosmos; lo imaginó como una conjunción coherente en la cual sus elementos se pueden contemplar como plenos cuerpos celestes, poseedores de organizaciones armónicas que propician que sus volúmenes interactúen entre sí. Esto ocurre en virtud de que sus magnitudes y proporciones, al girar, generan energías en intervalos que asemejan a los de la octava musical. Las esferas celestes de diáfana simetría emiten la celebrada “música de las esferas”, anteriormente inaudible al oído humano. Recientemente, la tecnología de la NASA ha logrado registrar los sonidos del espacio astral.

La “razón-armonía” refiere a las expresiones musicales como experiencias sensibles. A Pitágoras le interesó dilucidar la naturaleza imperceptible e inteligible de la música a través de secuencias numéricas, equiparables a la euritmia cósmica.

Todo universo armónico posee razones numéricas, y el conocimiento de estas razones haría posible comprender el “arqué” (origen) y los principios constitutivos de las cosas y las sustancias del mundo.

Los pitagóricos vieron en los números las leyes y proporciones que rigen los fenómenos naturales, lo cual permite develar el orden y la armonía que gobiernan el cosmos. Con el encuentro y la explicación de estas leyes y proporciones, se logra un conocimiento más exacto y veraz de las cosas de nuestro mundo.

El propósito unificador de la doctrina pitagórica se manifestaba en la relación entre el orden cósmico y el moral. Para los pitagóricos, el ser humano era también un microcosmos en el que el alma habitaba en la armonía del cuerpo. Por esta razón, entendieron que la medicina tenía la función de restaurar la armonía del organismo cuando esta se viera perturbada. Al ser la música el don armonizador para la purificación del alma, la consideraban —por sus propiedades— como una medicina para el alivio de la integridad física y anímica de los seres y sus entornos.

A través de Platón, diversas concepciones pitagóricas se convertirían en temas convergentes o polémicos de la filosofía occidental. Incluso en el siglo XVII, el genial astrónomo Johannes Kepler —quien descubrió las órbitas elípticas de los planetas— seguía considerando la visión de la polifonía del cosmos: la “música de las esferas”. Otros conceptos pitagóricos, como los de armonía y proporción, serían (y son) directrices fundamentales para la música y las artes visuales.

INFORMACIÓN COMPLEMENTARIA:

Las demostraciones matemáticas también son conocidas como demostraciones sin palabras.

El filósofo Martin Gardner de Tulsa, Oklahoma, en 1973, opinaba que las demostraciones sin palabras brindan la oportunidad de ser comprendidas de un vistazo y aseveró que, con frecuencia, una demostración árida y críptica puede convertirse en información amena gracias a las virtudes de visualizaciones geométricas (taxográficas) austeras, concisas, serenas y bellas, de modo que la proposición de un teorema se comprende a primera vista.

Los libros Proofs without Words: Exercises in Visual Thinking de Roger B. Nelsen y Icons of Mathematics: An Exploration of Twenty Key Images son obras ineludibles que versan sobre las demostraciones sin palabras y que han argumentado y visualizado de manera feliz sus bondades, allanando así su aceptación —o tolerancia— en los anacrónicos círculos de académicos rezagados, así como su difusión, divulgación y reconocimiento, tal como se hizo en la antigüedad.

Las demostraciones sin palabras no son realmente demostraciones matemáticas per se, sino otras posibilidades de experimentación y especulación, además de ser instrumentos nootrópicos. Los diagramas, esquemas o dibujos son visualizaciones que hacen posible comunicar y comprender los principios, la génesis y la demostración de los teoremas.

Los números poligonales

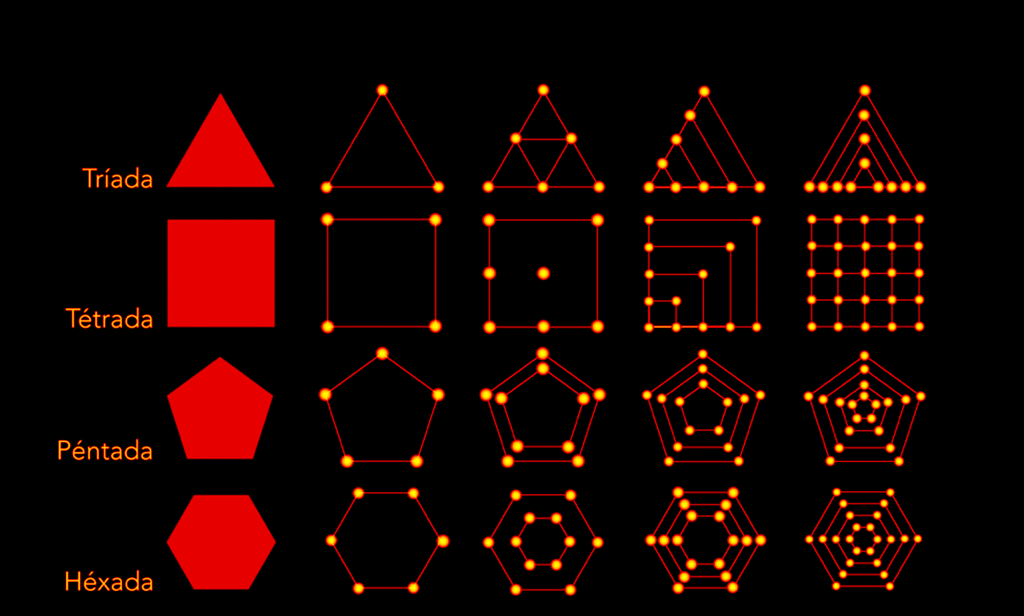
Los pitagóricos representaron los números mediante diminutas piedras que esparcían con gran celo en la arena, de modo que, al distribuirlas, formasen esquemas poligonales. Estas formas de organizar los puntos asociaban los números con los polígonos regulares: la disposición equidistante de puntos determinaba, por su adición, el número representado. Así se obtenían los diversos tipos de números poligonales:

Números triangulares: 1, 3, 6, 10, 15, …
Números cuadrados: 1, 4, 9, 16, 25, …
Números pentagonales: 1, 5, 12, 22, 35, …

Los números poligonales son visualizados en los inicios de la Comunidad Pitagórica como preeminente expresión de su visión mística numérica: no solo los entes son en esencia números, sino que los números son concebidos como entes. De manera que las expresiones “números triangulares”, “números cuadrados” o “números pentagonales” no son solo metáforas, sino que esos números son, en realidad —ante el espíritu, la mente y ante los ojos— triángulos, cuadrados y pentágonos: formas que son expresiones relacionales y referenciales.

La asociación del número con las imágenes geométricas (sintagmas) posibilitó a los pitagóricos la representación visual de los números, combinando las dos esencias que observan y visualizan las disciplinas matemáticas: las cifras y las formas. El imaginario de la fraternidad pitagórica reconocía en ambos atributos y relaciones equivalentes, por lo cual le otorgaron a la iconografía geométrica —sintagmas de los números— carácter y atributo de universalidad.

A los estudiosos pitagóricos, los números poligonales y su representación visual por medio de diagramas les permitían corroborar que cada número posee características singulares y plurales, a la vez que propiedades diferentes. Esto posibilita ver, a través de configuraciones geométricas (taxográficas), próximas a lo corpóreo y a la máxima exactitud matemática de forma geométrico-empírica, lo diáfano de las urdimbres relacionales consecución de sus hallazgos sobre cuadraturas, por lo cual a Pitágoras se le ubica en la cúspide del pensamiento matemático.

La multifiguración numérica les condujo a la expansión de conceptos aritméticos, así como a la universalización de la experiencia práctica, desarrollando lo que se conoce como atomismo numérico, que ilustra hermosamente la geometría de números multifigurados. Éstos, que son las primeras y más sustanciales estructuras de la geometría numérica, razón por la cual están en el epicentro de las matemáticas y se constituyen en la matriz prospectiva de la teoría de números.

Se veía en las galerías interminables, de elevados y gallardos cipreses a manera de frontispicios de museion, el benévolo albergue de la tibia y generosa brisa, alivio del candente crisol mediterráneo. Se procuraban infinitud de acanthus que ennoblecían peldaños y senderos, senderos conversos en elegidos espejos que reflejan la polifonía del entorno: los áureos ámbares de los amaneceres, la resonancia de la profundidad de los cielos, el resplandor de las efigies de sus andantes y la pirotecnia púrpura de la penumbra.
Se podía contemplar el magno brocado de los olivares, sus sombras arbóreas y ceñidos resplandores esparcidos por la mesiánica voluntad de Helios. Se podía ver con claridad el hondo aroma de los albos azahares, los extensos mantos de amapolas rubí levitando en el astral verdecer de su vibrante follaje, para cubrir la intimidad de las mieles de nuestra madre Gea. Ahí, en ese lugar que mira el esmerado oleaje de turquesas esmeraldas del mar Egeo; ahí, en ese místico escenario donde se es ungido de aristotélica inteligencia para imaginar coreográficamente la sublimada acústica de la música de las esferas; ahí, en ese lejano horizonte, es donde inicia la historia y la leyenda de las asambleas de sapientes aristócratas, posesos por la emocionante naturaleza de los conocimientos matemáticos y astronómicos, así como por la heurística de los bienestares.

De lejos, elaborar conjuntos de diversas configuraciones con guijarros repartidos sobre diminutos surcos pudo confundirse solo como un pasatiempo lúdico, semejante al que era habitual costumbre de los mercenarios al servicio de la república —bálsamo en sus escasas treguas—. La diferencia es de notar: la distribución de los guijarros sobre esquemas poligonales, trazados previamente en la incisa arena por los avezados integrantes de la enigmática comunidad de geómetras (taxólogos). Siglos después, se reconoce como un método de búsqueda, de construcción y comprobación de hipótesis, como uno de los instrumentos empíricos visuales heurísticos.

Los números poligonales han sido uno de los tópicos más emblemáticos de la historia de las arenas epistémicas de la aritmética, estudiados por matemáticos del calibre de Nicómaco, Diofanto, Mersenne, Euler, Gauss, Lagrange y Cauchy. Constituyen estratos de las raíces históricas de la teoría de números, manifestándose en numerosas esferas —ejemplo es el triángulo de Pascal—. Desempeñan un sobresaliente rol en el análisis combinatorio, participan en el binomio de Newton y en el cálculo de probabilidades, y han sido intensamente utilizados por Fermat, Pascal, Wallis y Roberval para la consecución de sus hallazgos sobre cuadraturas. Por lo cual, a Pitágoras se le ubica en la cúspide del pensamiento matemático.

El posible significado del Tetraktys pitagórico:

La Unidad: La divina perfección, la armónica unión origen de todo universo; la iluminación de la inmanencia del ser.
La Díada: Dualidad, conjunción; manifestación del principio masculino-femenino.
La Tríada: Los tres niveles del mundo —celeste, terrestre e infernal— y todas las trinidades.
La Tétrada: Los cuatro elementos (fuego, agua, tierra y aire), los cuatro referentes cardinales, los cuatro periodos climáticos del año solar, las cuatro dimensiones…

Razón por la cual, el Tetraktys (Τετρακτύς o Tetoakutes) pitagórico es el constructo emblema de la geometría (taxografía) que describe hipótesis y argumenta diversas tesis: la tierra original de la imaginada fuente de la Creación, la raíz por la cual se alimenta y sostiene la eterna Naturaleza, la armonía de los opuestos, la esencia numérica de las formas de todos los entes, los ciclos del eterno retorno; visiones que le dan sustento geométrico (taxográfico) a los 10 ámbitos, con los cuales patriarcas y rabinos visualizaron la estructura del Árbol de la Vida y del Conocimiento.

INFORMACIÓN COMPLEMENTARIA:
Centro Virtual de Divulgación de las Matemáticas
http://virtual.uptc.edu.co/ova/estadistica/docs/autores/pag/mat/Pitagoras11.asp.htm

Clasificación y denominación pitagóricas de los números
La música pitagórica y la teoría de las medias
La armonía de las esferas
El teorema llamado de Pitágoras
La divina proporción y el pentagrama pitagórico
El descubrimiento de las magnitudes inconmensurables
La cosmogonía poliédrica pitagórica
El Quadrivium pitagórico
El legado de Pitágoras: herencia y vigencia del pitagorismo
Epílogo: Pitágoras, filósofo y matemático
Bibliografía

COSMOVISIÓN: Visión del cosmos (mundo-realidad), percepción e interpretación del sentido de la existencia y de su entorno, nociones íntimas y sociales de la vida, de la naturaleza y de la cosmogonía.
La cosmovisión es ese complejo de opiniones, creencias, expectativas y razones signadas por la identidad de cada quién, los valores de comunidad y el espíritu de época. Toda expresión refleja la urdimbre del imaginario circunstancial que se constituye en trasfondos culturales.

TECNOLOGÍA COGNITIVA: Del griego téchnē (destreza/habilidad para la consecución de encomiendas), noción que refiere a instrumentos, recursos o procedimientos empleados para generar, potenciar, preservar, estudiar, comprender y comunicar, haciendo posible la satisfacción de necesidades y la realización de expectativas.

COGNICIÓN: Del latín cognoscere (“conocer”). Talento humano para analizar, inferir, deducir, relacionar, visualizar, prever, predecir, argumentar, valorar, referir, recordar, contextualizar y apreciar su realidad, la naturaleza, sus circunstancias y sus destinos.

DEVENIR: Del latín devenire (“acontecer”). Es el proceso de ser en el tiempo: continuidad y transformación en la permanencia; el antecedente que hace posible el porvenir.

PENSAMIENTO: Del latín pensare. Virtud humana para colegir, discernir, aventurar, relacionar, asociar, prevenir, avizorar, idear y representarse en la mente (imágenes) la realidad, alternativas y posibilidades en los porvenires.

VISUAL: Del latín visus, videre (“ver”). Sentido de la vista; experiencia sensorial óptica.

MATEMÁTICA VISUAL: Visualización de conceptos matemáticos mediante representaciones visibles, trazos, esquemas o modelos; demostraciones sin palabras de hipótesis o teoremas.

INTELIGENCIA: Del latín intelligentia (intellegere: “interpretar, elegir”). Máximo emblema de la humanidad. Es el ámbito de la mente que se manifiesta al optar, distinguir, proyectar, dimensionar, construir, crear, inventar, solucionar, valorar y apreciar.

Inteligencia visual: Para Platón y sus herederos, es el magno don: la habilidad de pensar, percibir y predecir a través de cavilaciones, observación y contemplación de situaciones, aconteceres, imágenes físicas o representaciones del mundo de las ideas.
La imaginación—visión mental (pensar con imágenes)—es el guion interno (inmanente) que permite describir el entorno experiencial y los objetos de la mente (ideas). Todos los seres humanos poseen estas destrezas en mayor o menor medida, pudiendo traducir ideas y conceptos a imágenes, las cuales también pueden transformarse mentalmente.

Las señas, los esquemas, los dibujos, así como los diagramas, los mapas, al igual que los planos, son visualizaciones, instrumentos con los que se puede proyectar y generar lo que antes era imperceptible e impensable.
La inteligencia visual-espacial es atributo de los elegidos: los profetas, visionarios, inventores y de los autores de los promisorios futuros. Pero también es inherente y posible en todo ser humano.

ESPACIAL: lo que está en relación con el espacio, que está o sucede en.
Inteligencia espacial: percepción y experienciación memorable e imaginable de circunstancias (continuo espacio/tiempo), así como de las características y de los atributos del entorno.
La inteligencia espacial se manifiesta por la destreza para describir, identificar y reconocer propiedades, relaciones, ubicación, postura, magnitudes, similitudes, coincidencias, cambios y diferencias en sus escenarios de estudio, actuación y contemplación.

IDEAS: del griego ἰδέα (aspecto, apariencia, forma), por extensión se relaciona con el término εἶδος (eîdos, ‘vista, visión, postura, posición, empatía e identidad’…).
Representación mental a partir de experiencias o razonamientos; es el producto de actos de interiorización y autorreflexión. Las ideas son actos y acciones de reconocimiento o descubrimiento, son aconteceres de autoafirmación, de interpretación, de conocimiento y de revelaciones heurísticas.

Las IDEAS son objetos mentales, creaciones del intelecto que refieren a los universos sensibles e inteligibles; son expresiones valorativas, propositivas y prospectivas, revelaciones de la imaginación.
Las IDEAS son intuiciones que se transforman en conceptos, en propósitos, en preceptos, en instrumentos para lograr versiones, bienestares y bienes sustentados en el conocimiento.

IMAGINACIÓN: del latín imaginatio, es el don de los seres para crear imágenes-visualizaciones mentales, que son configuraciones transitorias o permanentes, evocaciones y convocaciones para gestar obras del pensamiento, de la memoria, focalizaciones y construcciones interpretativas, al igual que invenciones, alucinaciones, sueños, y la preeminente gestión de la imaginación: ese altar de la humanidad, sus utopías.

SENSIBLE: experiencias-estímulos sensoriales registrados por los sentidos, por la sensibilidad.

INTELIGIBLE: del latín intelligibilis (inteligencia, intelecto, intelectual, mente, mental). Términos, nociones y conceptos que versan y refieren al universo de las ideas-formas, al εἶδος (eidos) platónico, a lo que define y explica a la naturaleza, a la existencia y todo fenómeno, acontecimiento y acontecer del devenir, del porvenir, dones, haberes, haceres y legados.
Las ideas-formas son delimitaciones-definiciones de transcursos, de dinámicas cognitivas y de secuencias de cognición: pulsión, volición, intuición, dilucidación, inteligibilidad, comunicabilidad.
Los conocimientos son logros de la mente, de la inteligencia, experienciación y raciocinio de atributos, coherencia y significación.

MENTAL: Lo que acontece en el interior de la mente; introyección y proyección en el universo del pensamiento, de la mente, de lo que esta genera, tamiza, pondera, aprecia, recuerda y ve a través de imágenes nítidas que son propuestas por sus pensamientos y por sus vivencias.

ÓPTICA: Refiere al ver, a la visión, a lo que es visible, lo que la vista experimenta, lo que a través de los ojos se presencia y comprende.

PULSIÓN: Describe los impulsos y proyecciones anímicas, volitivas y mentales para procurar, ejercer, realizar, trascender…

EURITMIA: Eurythmia, voz latina que hace alusión a la polisemia de los conceptos armonía, proporción, simetría, coherencia, concordia, concierto, belleza…

NÚMERO: del latín numerus, instrumento matemático que designa cantidades, cifras, extensiones, ubicaciones, conjuntos, fracciones, magnitudes, secuencias, periodos, referencias, relaciones, cálculos y contrastaciones.

SINTAXIS: Deriva del término griego syn (con) y taxis (orden); organización, relaciones, ordenación, conexión, reunión, coordinación, composición, estructura, forma…

FORMAS: Versión semántica que procede del griego μορφή (morphé, forma), material y simbólica, tangible e intangible; complejidad, interfaz contextual, estructura, características de ámbitos, conjunción de atributos, sistemas que modulan funciones y significados.

GNOSEOHEURESIS: γνῶσις (gnoseo, gnōsis, conocimiento) y εὕρηκα (héurēka), εὑρίσκειν (heurískein, hallar, inventar). Alusiones de la semiosis de la Grecia clásica correspondientes al conocimiento, a la teoría (visión) del conocimiento y a la heurística, a su génesis, a su creación, nacimiento, origen, generación, promoción; a la posibilidad de explicar su evolución: a la transformación del pensar, a los cambios graduales de visión, de principios, de fundamentos, de métodos, de alternativas de cognición; a la dinámica heurístico-cognitiva, a sus aportes, a la innovación, a los procurados beneficios, a la adaptación a los diferentes escenarios o eventos, a la trascendencia de sus circunstancias; al cambio de paradigmas, a la consideración de estos no como fronteras infranqueables, pero sí como puntos de encuentro y de partida hacia horizontes promisorios para nuestras civilizaciones.